Vertices of a Square

If $(6,9)$ and $(10,3)$ are the coordinates of two opposite vertices of a square, what are the coordinates of the other two vertices?
Source: NCTM Mathematics Teacher, October 2006

Solution

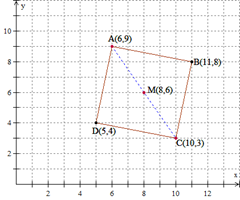
Let $A(6,9)$ and $C(10,3)$ be the two given opposite vertices of the square. The midpoint $M$ of both diagonals $\overline{AC}$ and $\overline{BD}$ has coordinates
$x=\dfrac{6+10}{2}=8$
$y=\dfrac{9+3}{2}=6$
Slope of diagonal $\overline{AC}$
$\dfrac{9-3}{6-10}=\textrm{-}\dfrac{3}{2}$
Slope of diagonal $\overline{BD}=2/3$ because the diagonals are perpendicular to each other.
By definition of a slope of $\textrm{-}3/2$ we move from $M(8,6)$ to vertex $A(6,9)$ by going left $2$ up $3$ . Similarly, by definition of a slope of $2/3$ we can count our way from $M$ to vertex $B(x,y)$ by going right $3$ up $2$ . Thus, the coordinates of vertex $B$ are
$(x,y)=(8+3,6+2)=(11,8)$
We find the coordinates of vertex $D$ the same way by going left $3$ down $2$ from $M$ . The coordinates of vertex $D$ are
$(x,y)=(8-3,6-2)=(5,4)$

Answer: $(5,4)$ and $(11,8)$

Alternative solution

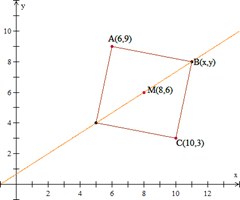
Let $B(x,y)$ be a vertex of the square. The point-slope form equation of segment $\overline{BM}$ is
$y-6=\dfrac{2}{3}(x-8)\qquad\qquad\qquad\quad (1)$
Length of segment $\overline{AM}$
$\sqrt{(6-8)^2+(9-6)^2}=\sqrt{13}$
$AM=BM$
$BM^2=13$
$(x-8)^2+(y-6)^2=13\qquad\qquad (2)$
Substitute the value of $y-6$ from Eq. $(1)$ into Eq. $(2)$
$(x-8)^2+[(2/3)(x-8)]^2=13$
$(x-8)^2+(4/9)(x-8)^2=13$
Factor $(x-8)^2$
$(x-8)^2(1+4/9)=13$
$(x-8)^2(13/9)=13$
$(x-8)^2=9$
$x-8=\pm 3$
$x_1=8+3=11$
$x_2=8-3=5$
Substitute the values of $x$ into Eq. $(1)$
$y_1=\dfrac{2}{3}(11-8)+6=8$
$y_2=\dfrac{2}{3}(5-8)+6=4$