Length of Segment

In triangle $ABC, AC=6$ and $BC=5$ . Point $D$ on $\overline{AB}$ divides it into segments of length $AD=1$ and $DB=3$ . What is the length of segment $CD$ ?

Source: NCTM Mathematics Teacher 2006

SOLUTION

Using the Heron’s area formula to calculate the area of triangle $ABC$
Area = $\sqrt{s(s-4)(s-5)(s-6)}$ where $s=(4+5+6)/2=7.5$
Area = $\sqrt{7.5(7.5-4)(7.5-5)(7.5-6)}$
$=\sqrt{98.4375}$
$=9.92$
$CE$ is the altitude of triangle $ABC$
Area = $\dfrac{1}{2}AB\times CE$
$9.92=(4\times EC)/2$
$EC=4.96$
Using the Pythagorean theorem in right triangle $AEC$
$AE^2+EC^2=AC^2$
$AE^2+4.96^2=6^2$
$AE^2=11.40$
$AE=3.38$
$DE=AE-AD$
$=3.38-1$
$=2.38$
Using the Pythagorean theorem in right triangle $DEC$
$DE^2+EC^2=CD^2$
$2.38^2+4.96^2=CD^2$
$30.27=CD^2$
$CD=5.5$

Answer: $5.5$

Alternative solution

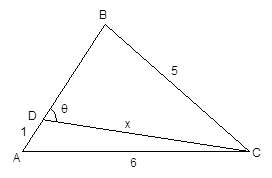
Using the law of cosines in triangle $BDC$
$5^2=3^2+x^2-2(3x)\text{cos}\,\theta$
$25=9+x^2-6x\text{cos}\,\theta\qquad (1)$
Using the law of cosines in triangle $ADC$
$6^2=1^2+x^2-2(1x)\text{cos}\,(180-\theta)$
$36=1+x^2-2x(\textrm{-}\text{cos}\,\theta)$
$36=1+x^2+2x\text{cos}\,\theta\qquad (2)$
Multiply Eq. $(2)$ by $3$ and add Eq. $(1)$
$25=9+x^2-6x\text{cos}\,\theta$
$108=3+3x^2+6x\text{cos}\,\theta$
———————————–
$133=12+4x^2$
$4x^2=121$
$x^2=30.25$
$x=5.5$